"Overunity" Devices by William J. McFreey - July 2013 By now, it is obvious to me that the so called "overunity" devices as demonstrated by Tariel Kapanadze, Floyd Sweet, Steven Mark, Don Smith, Alfred Hubbard, SR193 and others, draw their energy from the nuclei located in material which forms a part of the device. They are, in effect, conversion devices, converting excess energy of the nuclei to electricity and/or heat. In these devices, the fuel materials tend to be selected such as to have a non-zero spin, typically: copper, brass, aluminium, alloys of iron and the like. Therefore it has been speculated that Nuclear Magnetic Resonance (NMR) may play a significant role in the process of energy extraction from these materials through magnetic manipulation of their nuclei. In time, after many experiments, the conclusion was that the magnetic resonance alone, i.e. flipping of nuclei (transitions between various states of nuclear precession) with radio frequency, may only influence extremely unstable nuclei and make them beta decay (beta NMR). This phenomenon may be useful in some methods of energy generation, but the NMR method, in the case of power extraction from metals, suffers from some fundamental problems. In metals, the depth of penetration of RF energy is very limited due to eddy currents. This, in principle, limits the amount of volume of the material that experiences transitions between precession states. In general, it is accepted that only the spins of nuclei located in the skin layer of thickness take part in the resonance absorption of energy of the varying magnetic field. That is: For instance, the skin depth for copper is only about 0.2 mm at 100 kHz. The bulk of the material acts only as ballast although coupling of the Radio Frequency field in metals is normally enhanced by the generation of helicon waves (wikipedia). Fortunately, Radio Frequency is not the only method of inducing resonant nuclear transitions and Nuclear Magnetic Resonance can also be induced acoustically. In the presence of a constant magnetic field, as in the case of NMR, the Radio Frequency varying magnetic field also generates sound in conductive materials through eddy currents. The excited acoustic wave can in turn, interact with nuclear spins and acoustic NMR can be observed. The phenomenon is often called Nuclear Acoustic Resonance, usually abbreviated to “NAR”. The book “Nuclear Acoustic Resonance” by Bolef and Sundfors, describes both the theoretical and experimental aspects of this: (google books). Nuclear Acoustic Resonance is nothing more than an alternative means of inducing transitions between precession energy levels in nuclei with spin. The energy of mechanical vibrations (usually within the ultrasonic frequency range) is absorbed by the nuclei. At low amplitudes, Nuclear Acoustic Resonance is just another way of initiating magnetic resonance. The most effective technique is to create conditions for appropriate acoustic (mechanical) resonance of the energy gain material itself, where the amplitude of atomic vibration is significant. The vibration spectrum of the material has a characteristic standing-wave pattern, with individual graph lines corresponding to different mechanical resonant frequencies. If that is implemented, then, the value of the external magnetic field, in which the sample is immersed, has to be adjusted for acoustically driven transitions to occur. The higher the strain induced in the material, the higher the probability of transitions occurring. This paper clarifies the fact that nuclear magnetic resonance "NMR", which is understood to be resonant energy absorption by precessing nuclei, from either electromagnetic or acoustic sources, is not a necessary ingredient in the task of energy extraction from matter. Here, the precession is caused not by resonant absorption of EM or acoustic field, it is rather caused by energy of the rising magnetic field, exerting a torque on a magnetic moment of the nucleus that also has a spin property. This torque produces a change in angular momentum which has a component perpendicular to that angular momentum, causing the magnetic moment to precess around the direction of the magnetic field rather than settle in the direction of the magnetic field. This is called Larmor precession.The frequency of Larmor precession of the nuclei inserted in a magnetic field B is directly proportional to the value of the field as shown here: 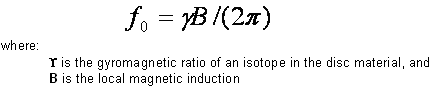(wikipedia) This is illustrated in Fig.1 and Fig.2a. Thus, to achieve sufficiently high frequency of precession, the value of B has to be raised sufficiently high. 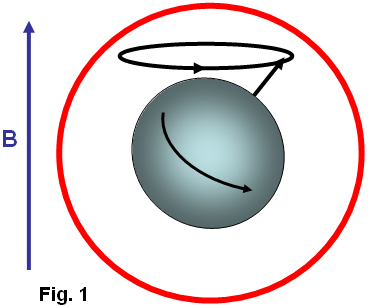Fig.1 shows the precession of a nucleus with non-zero spin inserted in a magnetic field B (not to scale). The red circle schematically represents the shell of electrons. Energy extraction phenomena are taking place when a precessing nuclei, immersed in magnetic field are also vibrated. Resonantly vibrating material can be viewed as a lattice of nuclei embedded in the shell and conduction electrons as shown in Fig. 2a. As the nuclei are much heavier than the electrons, the vibrating body will experience distortion of the electronic shell and displacement of the nucleus location within that shell due to periodic acceleration, as shown in Fig. 2b. If the resonantly vibrating material is immersed in a magnetic field, then, under certain conditions, a large number of it’s nuclei will be in precession. Under these conditions, an enhanced interaction between the precessing nuclei and the shell electrons may take place. It has to be born in mind that vigorous precession may also influence the shape of the nuclei. This enhanced interaction between the precessing nuclei and shell electrons under mechanical acceleration often results in transmutation of the nucleus and emission of fast sub-atomic particles (induced nuclear decay) in the plane perpendicular to B. The instantaneous proximity of the precessing nucleus to the electronic shell may be viewed as a collision of the nucleus and an electron (interaction between waves of matter). The phenomenon could be called the "intra-atomic grinding effect". It is interesting to note that the effect does not require large displacements of the nuclei from their equilibrium positions. A small displacement, being a small fraction of the atomic radius is capable of producing the effect. The displacement can be parallel, Fig.2b, as well as perpendicular to the magnetic field. Fig.2 shows that as the nuclei are much heavier than the electrons, any acceleration of the material causes the nuclei to lag behind, thus changing their position relative to the shell electrons. The arrows shown on the nuclei in Fig.2, represents their spin schematically, and the magnetic moment of the nuclei at a certain instant of time. The ellipsis above the nucleus represent nuclear precession. Symbol F denotes force. It is also worth noting that the magnetic field B, penetrating the energy-gain material, cannot be static. In a static magnetic field, the precession of nuclei ceases after a time period known as the spin-lattice relaxation time. After this time, most of the nuclei will align their magnetic moments parallel, or anti-parallel, to the magnetic field (e.g. for s = 3 / 2). To refresh the precession of nuclei, the field has to be brought to zero and then steadily, but quickly enough, increased to the desired value, such that the precession of a large population of the nuclei is maintained. This is easily achieved in an alternating magnetic field, or in a magnetic field oscillating between zero and some maximum value. The spin-lattice relaxation time is also called T1. Table 1 lists several metallic isotopes that can be of interest here. The T1 relaxation time tells us how long the precession of nuclei will last after induction. This is an important property. 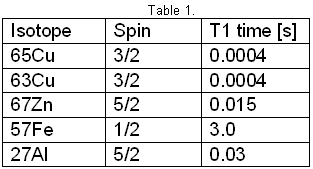The vibrating, spinning and precessing nuclei interacting with shell electrons invoke forced transmutation of the nuclei, releasing fast charged sub-atomic particles. The biggest advantage of this approach is that the shell electrons are already in close proximity to the nucleus and do not have to overcome the potential barrier created by the shell electrons as unlike the situation for external electrons. This specific vibration method of generating electricity from materials was ascertained by Michel Meyer in the Science et Vie 1976 article. In the caption of one of the figures in this article we read: Since the vibrating body is permeated by the magnetic field, the released fast, charged, sub-atomic particles will be deflected by the Lorenz force, FB = evB, forming a circular current in the energy-gain material. This current may resemble eddy currents, but contrary to the latter, it is constituted by fast moving charged particles, rather than slow electrons. This current arises very quickly and dies down quickly, as the electrons (or other charged sub-atomic particles) are either absorbed or radiated. The trajectories of these particles form short arcs rather than full circles. The rise and fall of the current in the energy-gain material produces a magnetic pulse which can be coupled inductively to a coil and used to do useful work. This specific vibration method of generating electricity from materials was ascertained by Michel Meyer in the Science et Vie 1976 article. In the caption of one of the figures in this article we read: " To shake the atoms and make them release the energy which they contain, you need to send a wave, with a high frequency oscillator (of the order of 172 kHz), that resonates with the vibration of the copper electrodes. This (is achieved) by an intermediary magnetic field that oscillates due to a coil surrounding the copper and connected to the oscillator ". (translation by William McFreey; The frequency of 172 kHz is the mechanical resonance frequency of a particular copper rod that Meyer was using at the time.). Moreover, Steven Mark in the presentation of his first "spool" device says "it vibrates ever so slightly". In another video, a co-worker of Mark, given the energised device remarks: "buzzing, vibration". It is also interesting to notice that Tariel Kapanadze's devices produce screeching or humming sounds. This is particularly noticeable in the video where the spool motor is demonstrated. In the 2004 device presentation humming and buzzing can be heard. Thus, shaking the atoms is quite common in the field of interest. Also, according to the above, NMR or NAR are not necessary in the process of energy extraction. What is needed, is a vibrating "energy-gain" material placed in an alternating magnetic field, or in more general terms, spinning and precessing nuclei periodically displaced from their equilibrium positions and immersed in a magnetic field. Mechanical resonance is not used here to induce nuclear precession, the nuclei are already precessing. The precession was established by the rising magnetic field. Mechanical resonance is used here to "shake" the nuclei and make them release the energy which they contain. There are many possible implementations of the principle described here. Physical shape and the appropriate frequencies of oscillation in these implementations will depend on the form and size of the "energy-gain" material. The simplest, intuitive implementation of this idea is shown in Fig.3 which shows the concept of an electromechanical transmutation device (symbol F denotes a fuse): 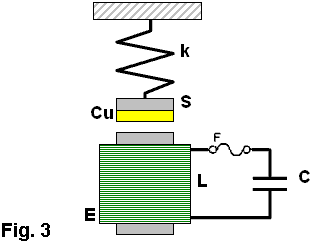Here, a disc of copper, Cu, laminated to the magnetic steel disc S, and attached to a spring k, is fixed above an electromagnet E of inductance L which forms an L-C circuit in conjunction with the capacitor C. The steel part of the laminated disc S is magnetised by the core of the electromagnet E. At the same time the magnetic field between the steel disc and the electromagnet core permeates the copper disc. The higher the current through the electromagnet, the stronger the field in the copper disc becomes and the greater the attractive force between disc S and the core E. It is, of course, understood that the initial oscillations are invoked externally, e.g. by momentarily charging the capacitor C. Since the attraction force between S and electromagnet core is independent of the core magnetic polarity, therefore, the frequency of mechanical force on the plate S will be twice that of the frequency of current maxima through the electromagnet. Thus for the system in Fig.3 to oscillate in an electromechanical resonance, the frequency of electrical oscillations of the LC circuit should be tuned to half the frequency of the mechanical oscillations of the composite disc. Whenever the field in Cu, the gain material, crosses zero, the magnetic moments of the nuclei take random orientation. When the field starts to rise, the magnetic moments try to orient themselves along the field. However, because the nuclei also have spin, the torque on the magnetic moments will cause the nuclei to precess. This precession will be fastest at the peak of the magnetic field. At this point. the acceleration of the Cu disc will also be greatest. This will shift the precessing nuclei position, to interact strongly with shell electrons, and forced transmutation will occur. The ejected electrons will then form a strong current pulse, as discussed above, which will be coupled by electromagnet coil L and pulse charge the capacitor C. This will increase the current flowing in the electromagnet in the next cycle of the electrical oscillation, which in turn, will increase the amplitude of mechanical oscillation. This process will repeat itself to the point of the system destruction at the expense of the energy from Cu transmutation. To prevent the self destruction, it is advisable to connect the spark-gap across the LC circuit to discharge (waste) the excess energy thus maintaining the electromechanical oscillations at the safe level. Excess energy can also be coupled by few turns of winding wrapped around the electromagnet and utilised. It should be understood that the amplitude and frequency of mechanical oscillations of the composite disc have to be sufficiently large to provide large enough acceleration of the nuclei. Since in harmonic motion of a mass m attached to a spring of modulus k is a = -Aw2 (A-amplitude of oscillations, w-angular frequency), sufficiently high values of acceleration can be achieved either by increasing the amplitude or the frequency of mechanical oscillations. It is immediately noticeable that increasing the frequency is more effective in this case. This requires a spring with relatively high value of k and low values of m: w2 = k/m. A more practical and improved implementation of the same idea is presented in Fig.4: 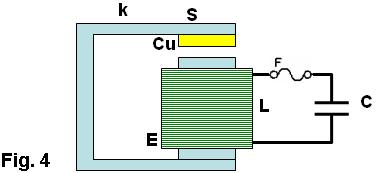Here the spring is made of magnetic steel in the form of a U-shape. This U-shape also works as a magnetic guide. Yet another possible implementation of the above idea is even more intuitive. It consists in placing one of the turns of a coil inside the coil. In this arrangement, the coil L also forms an L-C circuit in conjunction with the capacitor C, as shown in Fig.5a where a single turn of a coil winding is placed within the coil: 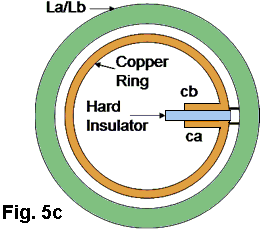Here, the schematic layout is shown in Fig.5a. The single-turn ring resonator is shown in Fig.5b, and the top view of the arrangement is shown in Fig.5c. The connecting wires to the ring resonator are marked as ca and cb respectively. The hard insulator also supports the ring mechanically. Vibration of the ring is marked by double sided arrows V shown in Fig.5b. The gap between coils La and Lb is only shown to help with visualising the way that the coils sandwich the ring. In reality, the coils touch one another and the ring is placed inside, not actually touching the coils. Alternatively, coils La and Lb can be fitted with cores and the ring may than be placed in the gap between those cores, but not actually touching the cores. If this single turn (in general, it can be more than one turn), is made of brass or copper and is prepared so as to form a ring, (as indicated in Fig.5b), then the turn will form a mechanical ring resonator. The direction of vibrations in this ring is marked by double sided arrows (one of them marked V). Since the ring is part of the coil winding, the current oscillating in the L-C circuit will, of course, also flow through the ring. Owing to the fact that the ring is immersed in the magnetic field of the coil, the mechanical vibration of this resonator will be excited by the Lorenz force which will try to expand or shrink the ring radially. The frequency of this force will be twice the frequency of the oscillations of the L-C circuit. This is because when the current flowing through the ring changes direction, the magnetic field in the coil also changes direction. The ring's fundamental resonant frequency corresponds to the mode in which all the points of the ring move radially outward together and then radially inward together. This is analogous to the fundamental longitudinal oscillation mode of the rod. Thus, the resonant frequency fr of ring vibrations is: fr = vL/Pi.d, where vL is the longitudinal speed of the sound wave in the material of the ring (e.g. copper), Pi is 3.1415926535 and d is the diameter of the ring. The speed of the longitudinal sound wave in copper is approximately 4 km/s. So, for a copper ring 10 cm in diameter, the mechanical resonant frequency of the ring will be around 12,730 Hz. The L-C circuit will then have to be tuned to 6,365 Hz for electromechanical resonance to be established. When the electromechanical resonance is established, and the amplitude of oscillations is high enough, pulses of fast electrons are generated in the ring, which in turn generate magnetic pulses, as described above. These pulses are coupled by the coil itself, recharging the capacitor C. This way, once started, the oscillations will gather strength until the circuit self destructs. To prevent self destruction, the circuit has to be fitted with a dissipative mechanism such as a spark-gap (a fuse may also be useful) or an automatic detuning mechanism that leads to the condition where the L-C circuit oscillates on a frequency slightly different to fr / 2. The latter mechanism has been described by Mandelstam and Papalexi (see Mandelstam, Papalexi, 1935). In their original method, detuning the electrical oscillation frequency from that of the mechanical oscillations was found to utilise the magnetic saturation effect in iron, but nowadays ferrite can also be used in this application. In the electromechanically resonant system shown in Fig.6, an inductor Lc, wound on two ferrite toroidal cores, is connected in series with coils La and Lb. Coil Ld, is wound on each core in opposite directions to minimise coupling from Lc to Ld, forming a magnetic biasing coil. In this way, the L-C circuit, consisting of components La, Lb, Lc, and C, can be tuned by passing current through Ld. The automatic detuning loop starts with coil L2 which is magnetically coupled to La/Lb, which feeds the bridge rectifier. The rectified signal, after filtration by C1, supplies the biasing current to Ld. Thus, the higher the amplitude of oscillations of the L-C circuit, the higher the current in Ld and therefore the higher the magnetic saturation of the toroidal cores. Magnetic saturation of the toroidal cores reduces the inductance of Lc and detunes the oscillation frequency of the L-C circuit. This, in turn, reduces the amplitude of ring vibration and the conversion rate (the rate of transmutation) in the ring. Coils L3 form a filter, preventing spuriously coupled RF by Ld from overloading the system. Diode D1 increases the feedback threshold. In fact, D1 may consist of several diodes connected in series or be simply a Zener diode. Coil L4, is also magnetically coupled to La/Lb, and couples usable energy. This energy can be used directly, as shown in Fig.6, or after rectification, used as a DC source. Drawing more power from the device, normally reduces the current flowing through Ld and diminishes the detuning between resonances, increasing the conversion rate. Instead of the ring one may use a section of tubing with a slit. In this case, however, coils La/Lb should not be wound directly on the tube as this would prevent mechanical vibration of the tube which is essential if transmutation is to occur. The tuning procedure for this device consists mainly of determining the resonant frequency of the ring vibrations, fr, and then adjusting the value of C so that the (La,Lb,Lc) - C combination resonates at the frequency fr/2. Fig. 6 shows a schematic layout of the "resonance-in-resonance" generator with feedback. The feedback detunes the frequency of electrical oscillations from that of the mechanical resonance. A single toroid tuning coil may also be used provided that it is wound properly 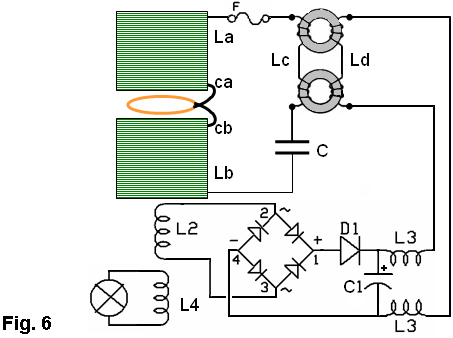The device concepts shown in Fig.4, Fig.5 and Fig.6 can be classified as "resonance in resonance" or electromechanical resonance devices where both mechanical and electrical oscillations are caused by just a single current flow. This current, being part of the electrical oscillations, also excites the mechanical vibrations. Part of the energy of electrical oscillations feeds the mechanical vibrations. Thus, this is a closed loop system. These kind of systems can easily be transformed into toroidal power units (TPUs) by choosing an appropriate diameter for the coils La/Lb and for the excess-energy ring. The system shown in Fig.6 can be started by disconnecting the load from L4 and briefly connecting a frequency generator to L4. The other method of starting the device would be to momentarily charge the capacitor C, with the load disconnected. One can also envisage an open loop system which works on the same principle: vibrating body placed in an alternating magnetic field. Here, however, excitation of the gain medium vibration, and generation of the varying magnetic field are separated. An example of an open loop generator is shown in Fig.7 in which the gap shown between coils La and Lb is for clarity only, unless the coils are fitted with ferromagnetic cores. Transformer T supplies low frequency (LF) alternating magnetisation current, (f = 50 to 4000 Hz) to coils La and Lb through coil L1 which is wound using heavy gauge, well isolated wire: 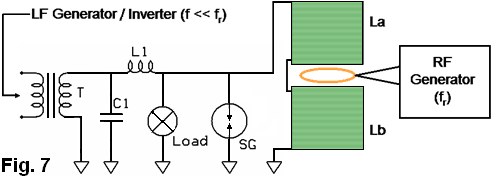The ring resonator placed within the magnetic field of La/Lb is resonantly vibrated by strong pulses of current from a Radio Frequency generator (fr = 2 - 200 kHz). The frequency of these pulses should be equal to fr and preferably be an integer multiple of the coil magnetisation frequency f (fr = nf, usually n > 6). Since the field in La/Lb is modulated, the amplitude of ring vibration also varies, being smallest at field transitions through zero and highest at magnetic field maxima. Forced transmutation of nuclei in the ring material occurs near the field maxima and manifests itself as strong magnetic pulses, as described above. These magnetic pulses are coupled by La/Lb in the form of high voltage spikes across the coil. These spikes power the load, but are filtered out by L1- C1, preventing unwanted feedback to the LF generator. In a well designed system, instead of an LF generator-T combination, the direct output of a power amplifier can be used. Self powering in this open loop system is possible by drawing some power from the coil, transformation, rectification and filtration. The DC power thus obtained can be used to supply the LF and RF generators. The spark-gap SG limits the excess voltage on the coil, preventing damage to the load. The process of tuning of this device is even simpler and consists of determining the resonant frequency of the ring vibrations fr, and then adjusting the frequency and value of the LF magnetisation current in coils La/Lb until the Load is powered. The frequency fr which is the mechanical resonance frequency of the ring, has to be maintained during operation of the device. In an alternative method, the tuning can be accomplished in situ, without prior determination of the resonant frequency of the ring. At a given magnetisation current through coils La/Lb, one can simply sweep the frequency of the current pulses exciting the ring, looking for sparks in the spark-gap or maximum output power on the load. The procedure can be repeated at various values of magnetisation current. A simple analogue (not digitally tuned), widely tuneable pulse generator with power transistor output is sufficient for the task. Actually, sweeping the frequency fr is a necessity in this system during operation of the device, although this is only done over a very narrow frequency range. This is because mechanical resonance frequency of the ring resonator is very "sharp" and so it is not possible to maintain that exact frequency for a prolonged time interval. The sweeping across this narrow frequency band has to be synchronised with the magnetisation current. As mentioned before, the range of resonance excitation frequencies depends strongly on the physical dimensions of the energy-gain material. Here, we considered energy-gain resonators whose size is of the order of centimetres. However, if the energy-gain material is in the form of a powder, as for instance in the Colman/Seddon-Gillespie tube shown earlier in this chapter and further detailed at the web site of RexResearch, these tiny multiple resonators are just micrometers in size, and so their resonant frequency of oscillation is very high, being of the order of hundreds of megahertz. Additionally, when in powder form, the skin effect does not pose a significant limitation. Similarly, the frequency, f, of the magnetisation current, as in Fig.7, has to be chosen carefully. As can be seen in Table 1, for copper, the precession lasts for only 0.4 milliseconds after excitation. Magnetic field rise time, from zero to it's maximum value, at 50 Hz is 5 ms. Thus, for some nuclei (e.g. copper), with magnetic field oscillation at 50 Hz or even 60 Hz, the rise-time of the magnetic field, may be too slow to sustain the precession of large number of nuclei and therefore, no energy will be released under those circumstances. At low magnetisation frequencies, aluminium or alloys of iron may be a better choice for the ring or tube. This paper concentrates on the vibration method of energy extraction from metals. On the other hand, in dielectric materials, solids, liquids and even gases, such as nitrogen, the nuclei can be vibrated electrically, through polarisation. In that case, no explicit mechanical vibration may be required for energy extraction. The connection of the ideas and examples of devices described here to the devices presented by some inventors should be obvious to those familiar with the technology. It is quite possible that Nikola Tesla experimented with this technology a long time ago. Please be fully aware that this analysis is for information purposes only and must not under any circumstances be considered to be a recommendation for the reader to build or experiment with any such device as lethal voltages are liable to be generated by the coils. Radioactive particles may be produced by this device. It may be necessary to mount any such device in an earthed box made of aluminium (or other suitable metal) in order to screen out any stray radioactive particles. The fuel ring or disc must be connected to ground because the voltage generated in the ring or disc can get very high and pose a danger of a fatal electric shock. The disc, ring or tube may overheat and might even explode. Thus it is entirely your own responsibility should you decide to experiment with this kind of device. The principles of operation of Kapanadze electromechanical devices by William J. McFreey - February 2012 Two recently released (although old) YouTube videos: here and here, show a motor or electromechanical device designed by Tariel Kapanadze, running self-powered with a major mechanical output after being started with a tiny PP3 nine-volt battery only capable of providing a small current. The following analysis shows that Tariel’s device is in fact, a motor whose torque is generated by forced transmutation (wikipedia) as shown here: 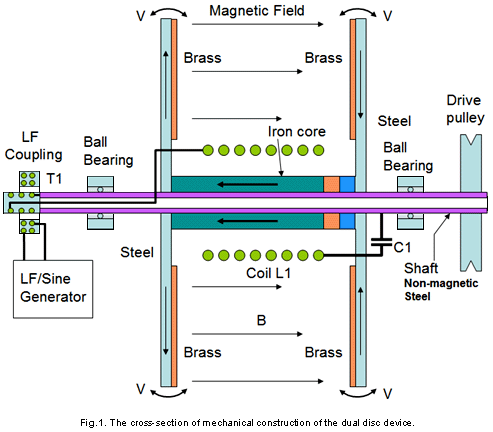Some of the actual implementation details may differ from the arrangement shown above, but that should not alter the operation of device. The drawing above is not to scale. The device consists of two identical composite discs mounted opposite each other on a shaft. The discs are connected by transformer-style laminated iron shims (to suppress eddy currents) or by a ferrite core. The core may actually include permanent magnets within it. This core, which is marked with arrows in the drawing above, is mounted on the shaft and positioned between the plates and in conjunction with the coil L1 and a magnet it provides the necessary static and varying magnetic fields between the steel flanges. Each disc consists of two materials: brass (or possibly copper) and magnetic steel. The brass parts of the discs face each other. The external rotary transformer T1, is used to deliver low-frequency energy to the resonant L-C circuit consisting of coil L1 and capacitor C1. This form of construction provides, not only the varying magnetic field between the flanges, but also a cylindrical symmetry of that field. The magnetic field passing though the brass plates is strongest at the outer perimeter of the discs due to the fact that the magnetic flux tends to exit the steel flanges near their perimeter, while it is strongly guided within the flanges, so the length of the black arrows in Fig.1, symbolically represents the strength of the magnetic field at that distance from the axle. The exact distribution of the field between the plates will depend on the geometry of the device, magnet strength, flange material, flange thickness and plate separation. In other words, the two steel flanges create a radially symmetrical and, in general, increasing distribution of the magnetic field. Fig.2 presents an example of magnetic field distribution between the steel flanges as modelled with FEMM (www.femm.info). 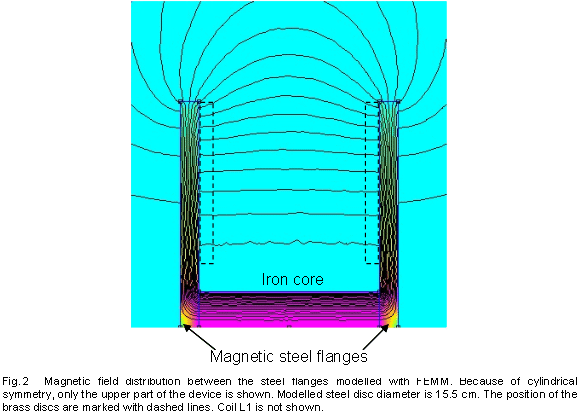Plots of radial magnetic field distribution, starting from the magnet perimeter are shown in Fig.3: 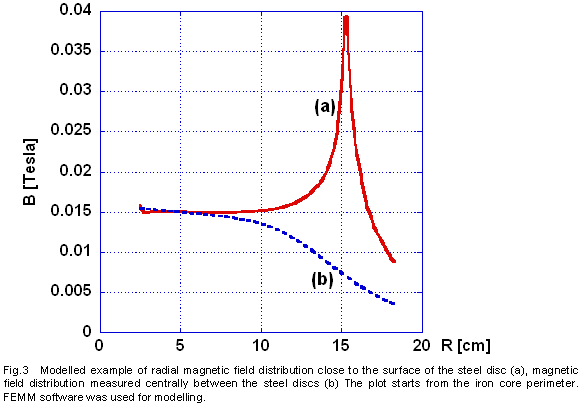Trace (a) represents the value of B close to the steel flange surface (within the volume of the brass disc). Trace (b) plots the distribution of B measured centrally between the steel discs. It can be seen that trace (a) is almost flat for radiuses ranging from the core perimeter to the middle of the disc. Each brass disc in this arrangement can act as an enhanced transmutation device. There is a magnetic field perpendicular to the flanges and the strength of that field is circularly symmetrical within the volume of the brass discs. As an approximation, you can visualise it as there being a very large number of “cylinders” of equal magnetic strength between the flanges. The brass discs are immersed in this varying magnetic field. To excite this magnetic field, an externally generated low-frequency input signal is transmitted through the rotary LF coupling transformer T1, to the L1/C1 resonant circuit. The signal returns through the steel plates and the non-magnetic shaft. The magnetic field created by coil L1 is therefore oscillating at a frequency of f = VL1 x C1 x Pi / 2 (the inductance of the secondary winding of the transformer T1 is ignored here for simplicity). Since this device is arranged as a high-Q L-C circuit, the current in the coil and therefore the magnetic field strength between the flanges can achieve very high values even with low power excitation. The question now is: how is the torque created in this device? To answer this question, one has to resort to basic physics. First of all, it has to be noted that this arrangement of plates also creates a high-Q mechanical resonator. Namely, two circular plates supported in the centre. The fundamental mode of oscillations in this device is where the outer perimeters of the flanges come closer together and then move further apart in a periodic manner as marked by the double headed arrows V, in Fig.1. The plates can actually vibrate in many different modal patterns, sometimes called "Chladni Patterns" in honour of 18th century scientist Ernest Chladni. This situation is complicated by the fact that the plates are composite and not a uniform material. Here, we assume that the plates vibrate in their fundamental mode. The vibration of these plates is caused by the current flowing in coil L1. The higher is the current in L1, the stronger the magnetic field strength becomes and as a result, the attraction force between the flanges increases. This periodic force makes the flanges vibrate. This periodic oscillation of flanges creates periodic acceleration of the brass (or copper) material bonded to the steel plates. The highest acceleration experienced by brass is when the magnetic field strength between the plates is highest. The current in the coil and mechanical vibrations are highest under electromechanical resonance, i.e. when the frequency of the L-C oscillations coincide with half the resonance frequency of the vibration of the plates. Here, however, for reasons explained later, the magnetic field is not alternating, but rather oscillates between zero, or close to zero, and some maximum value. For this reason there is a constant bias of the field between the flanges, created by a permanent magnet, (marked blue and red in Fig.1), attached to the core connecting the flanges. This arrangement needs the frequency of the L1-C1 combination to match the frequency of the mechanical oscillations of the flanges. The nuclei of the atoms in the plates have non-zero spin, and since they are charged, they also have a magnetic moment. The spin of the nuclei is of foremost importance here. In the presence of an applied external magnetic field B, the magnetic moment of each nucleus experiences a torque that tends to align it parallel with the field. But the nucleus has also the spin property and therefore enters into precession at an angle theta about the axis of the magnetic field (wikipedia). The frequency of this precession is given by: 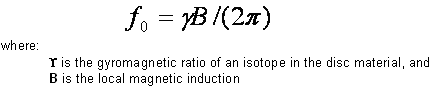(wikipedia) In this scenario, under electromechanical resonance of the flanges (which are the energy-gain material), when the amplitude of mechanical oscillations is high enough, the spinning and precessing nuclei in the medium interact strongly with the shell electrons (an intra-atomic grinding effect), causing the nuclei to transmute. In the transmutation event, fast electrons, or other particles, are emitted in the plane of the disc. These electrons are then deflected by the Lorentz force and they constitute the circular current (Fig.4), with a radius: 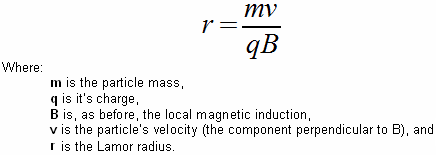This current arises very quickly and dies down quickly, as the electrons are absorbed or radiated (as described in the preceding article). The rise and fall of the current in the disc produces a magnetic pulse which can be coupled inductively by a coil and may do useful work. Here, however, the magnetic pulses are being partially coupled by coil L1, thus increasing the amplitude of the oscillations and reducing the amount of input energy required from the generator. To be useful in this process, the nuclei must possess a non-zero spin. After transmutation, fast electron (or other particle) emission event, the spin of the nuclei generally decreases or vanishes completely. For instance: 69Cu(s = 3/2) -> 69Zn(s = 1/2)+ e- + v + E. (this is only an example, and so it does not mean that this reaction is taking place here). This change of spin is transferred to the material surrounding the nucleus and torque is created in the disc. Thus this phenomenon causes the spool device to become a motor. The constant bias of the magnetic field between the flanges makes sure that only one type (direction) of spin is converted to rotational energy. 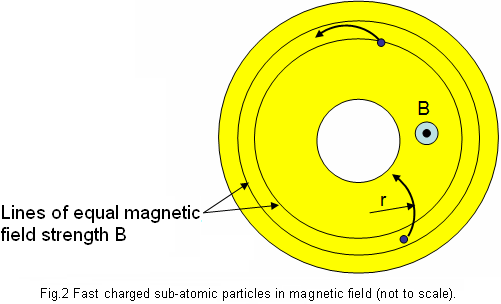As can be noticed in the videos, one of the discs is coated on the outside with a foamy substance. This substance hides the high voltage capacitor C1 or a bank of high voltage capacitors that constitute C1, and at the same time reduces the amplitude of vibrations of this flange. Nevertheless, occasional screeches can be heard when the device is being started. In conclusion, the Kapanadze disc machine works on a principle of spin manipulation, precession, vibration and induced transmutation. The choice of materials for the flange and disc construction is of extreme importance. In the flanges, magnetic steel is used to provide both strength and an even distribution of the magnetic field. For the discs, brass, which is an alloy of Zinc and Copper is used as both of these have many isotopes with non-zero spin (wikipedia). It should be added here that the device described by Mandelshtam and Papalexi in their famous 1935 paper (Technical Physics of the USSR, Leningrad; Volume 2, Number 2-3, pp 81–134, 1935) works on the same principle described here. Although, the authors do not state this explicitly, the device produces excess energy through reactions taking place in the rotating and at the same time vibrating disc (the vibration is induced by eddy currents). The authors concentrate only on parametric excitation of oscillations using the described method. No wonder, Nuclear Magnetic Resonance was first described and measured in molecular beams by Isidor Rabi only in 1938. The only additional feature is the segmented disc used by Mandelshtam and Papalexi, as opposed to the uniform disc described here, as their arrangement also parametrically generates the LF oscillations that makes the magnetic field oscillate within the segments of the rotating disc. The physics behind all of Kapanadze’s devices is the same and very interesting. It is stressed however, that no laws of physics, as we know them today, are violated here. The fuel is supplied by the material of ring or disc. The devices will not work forever and it is not free-energy, nor overunity (depending on how that is defined), but they are remarkable, both in their engineering and architecture. These types of device were invented or reinvented by Michel Meyer in the early 1970s (as can be seen earlier in this chapter and at RexResearch), and developed further by Steven Mark in the mid 1990s. It is also possible that Nikola Tesla, and then Alfred Hubbard, experimented with this kind of device. This analysis is for information purposes only and must not under any circumstances be considered to be a recommendation for you to build or experiment with any such device. Radioactive particles may be produced by this device. The centrifugal forces may become extremely high in this device and so it is your full responsibility if you chose to experiment with this device. It may be necessary to mount any such device in an earthed aluminium box in order to screen out any stray radioactive particles.